この記事は, 理情 Advent Calendar 2024の12/6の記事です. この文章を読むのに飽きたら是非他の人の書いた記事を読んでみてください.
はじめに 見出しへのリンク
今年4月ごろに, 元から興味を持っていたプログラミング言語もとい定理証明支援系のLean4に満を持して入門しました.
しかしながら, 単に情報がないからなのか自分の検索能力が低いからなのか, 普通に手元では証明できているのにLean4にどのように書き下せばいいのかわからない場面が何度もあったので, この記事では初心者なりにかなり便利でもっと早く知っておきたかったいくつかのトピックを, 少しでも証明を楽しむためのヒントとして記したいと思います. かなり雑多だと思うのですが, どうかお付き合いください.
注意点として, Lean4の公式の Theorem Proving in Lean 4 に載っている内容はこの記事では基本省略してあるので, 基本的な使い方を習得するのにはこの記事は向かないと思います.
また, 直観論理の世界から抜け出したくない方には申し訳ないのですがこの記事では古典論理を前提としており, 断りなくopen Classicalされていることを仮定しています.
1. Lean 4 VSCode Extension 見出しへのリンク
かなり当たり前かもしれませんが, この拡張を入れるとLean4のsyntax highlightingや入力予測がされるようになります. それだけでなく, 現在の証明の流れがとても掴みやすくなるInfoViewが見れるようになります.
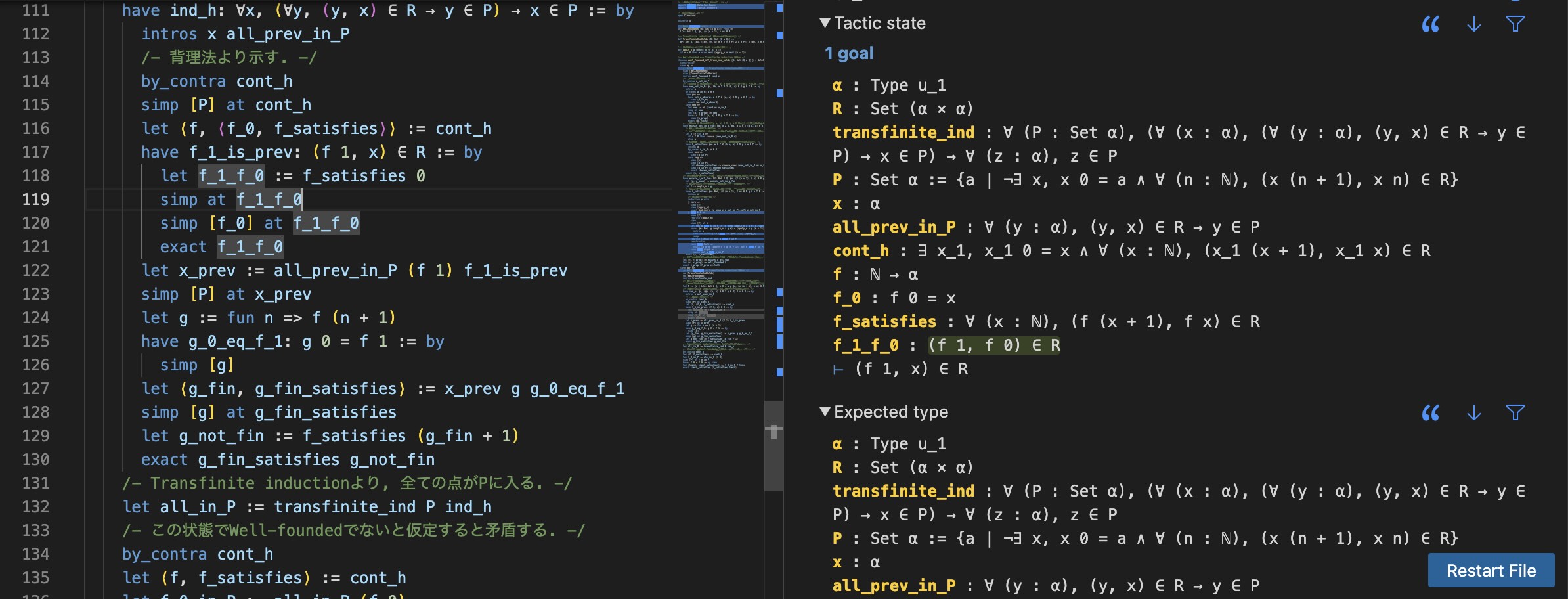
左に書かれているのがLean4の証明で, 右がその様子をわかりやすく表示してくれるInfoViewです. 写真では119行目にカーソルが合っているので119行目における証明の進行状況が表示されています.

このviewの見方をざっと解説します.
まず, 画像でオレンジ色で表示されているのが, すでに導入された命題のリストです. 仮定として証明に使って良い名前付けされた命題が並んでいます. Curry-Howard同型対応と呼ばれる, ざっくりといえば関数と型はそれぞれ証明と命題に対応するという対応関係から, 現在のスコープにある変数とその型であるとみることもできます.
次に画像で一番下に表示されているのが, この証明のゴール, つまり示すべきものです. このゴールは, 必ずしもある定理の証明をする間ずっと同じというわけでもなく, 場合分けの途中や補題の証明中などに変わることもあるので, 今自分が何を示そうとしているのか意識するためにも常に把握しておきましょう.
最後に, 画像の中でうっすら緑色で表示されている部分が今カーソルを合わせている行によって変更された点です. Lean4の証明はゴールを書き換えたり仮定を書き換えたり付け加えたりして証明を進めていき, 自明な形になるまでこれを繰り返します. この例では仮定をsimpによって書き換えた結果が表示されています.
ここまでVSCodeの拡張の話になってしまいましたが, Neovim等用いられている方も同等の機能を持つ拡張を探してくるととても捗ると思います. 私はまだVSCodeから卒業できていないので詳しくは知りません.
2. Mathlib4 見出しへのリンク
Mathlib4はLean4のコミュニティが作成しているLean4のライブラリのようなものです. このMathlib4には, よく用いられる定義や定理などが収録されています.
有名な定理や一般的な定義くらいは自分で定義せずとも扱えるようにしたい方にはとてもおすすめです. 前提はMathlib4からの引用に任せて, より本質的な問題に集中できるので時間の節約にもなります.
もちろん, ライブラリに頼らず全て自分で定義して証明したい硬派な方はMathlib4に頼らなくても全く問題ないですが, 完全に頼り切らないにしても, 「便利なtacticsを追加してくれるものとして証明の依存関係に入れておく」くらいの距離感でも十分便利なのでお勧めしたいです.
導入方法はMathlib4のGitHubから見ることができます.
GitHub: https://github.com/leanprover-community/mathlib4
以降, 断りなくMathlib4に含まれるtacticsも利用します.
3. Mathlib4のdocument 見出しへのリンク
https://leanprover-community.github.io/mathlib4_docs/
先述のMathlib4ですが, あまりにたくさんの定義や定理が収録されているので, 自分の使いたいものの定理の名前は何か, そもそも収録されているのかどうかなどがわからないことがあります. そこで使えるのが上記のリンクから飛べるドキュメントです. サイトのリニューアル等が考えられますが, 執筆時点(12/6)ではサイトの左側にある定理や定義が分野ごとに纏められたアコーディオンメニューと, 右上に検索欄があり, そこから自分の探したいものを探せるようになっています. 一応, Mathlib4以外にも標準で搭載されている定義や定理も参照できるようになっています.
試しに関手の定義を調べるとそれぞれ以下のように出てきます.
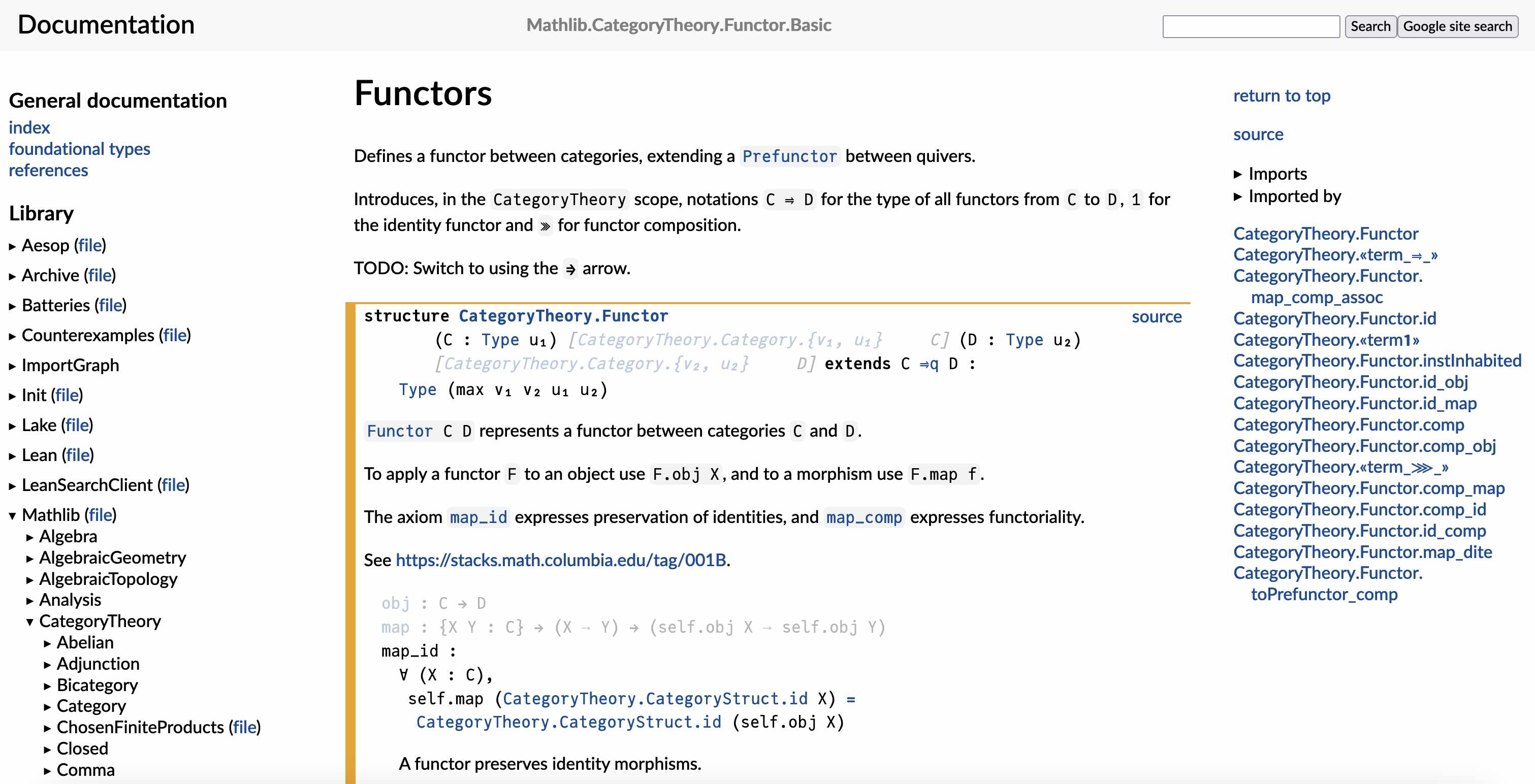
Mathlib4ではなく標準ライブラリに入っている自然数の足し算の可換性の定理を調べてもちゃんとヒットします.
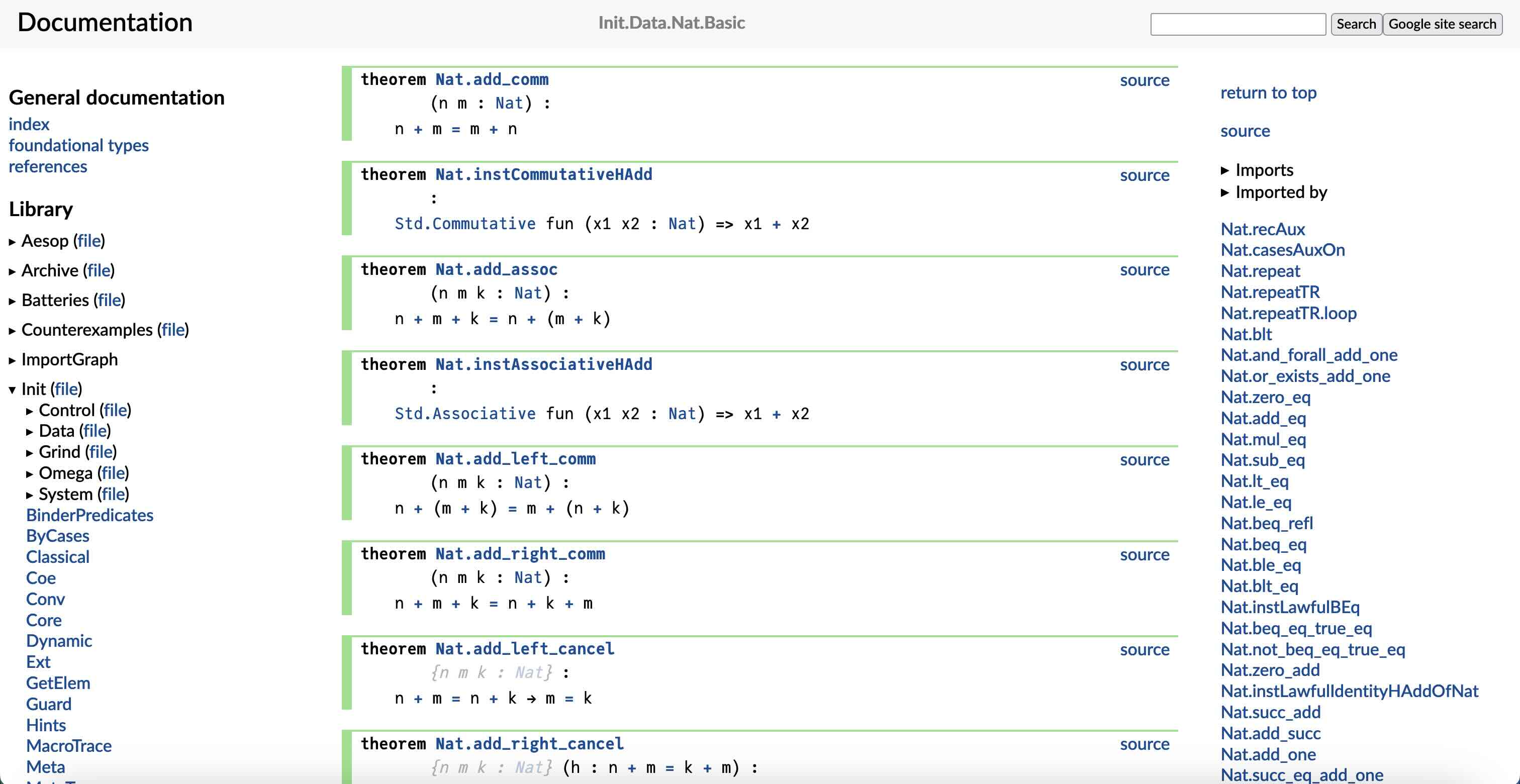
余談ですが, 私自身どのように検索するのが効率的なのかがいまだにわかっておらず, 必要な定理の検索の際は, 適当に分野を絞り込んでから「これまで目にしてきた定理の命名規則から推察してこのような名前をつけるはずだ」とアタリをつけて調べているので, かなり骨が折れる作業となっています. もし, どのようにすれば欲しい定義・定理を調べられるのか知っている方がいれば教えていただきたいです.
HaskellにおけるHoogleみたく型で定義や定理を検索できるならばかなり嬉しいのですが. これは作る機運…?
4. Anonymous constructor 見出しへのリンク
Anonymous constructor自体はドキュメントでも紹介されているので軽く紹介します. 例えば, Anonymous constructor⟨...⟩を用いれば以下のように∧や∃などを導入できます.
theorem intro_and: A → B → A ∧ B := by
intros a b
exact ⟨a, b⟩
theorem intro_exists {P: Nat → Prop}: P a → ∃x, P x := by
intros P_a
exact ⟨a, P_a⟩
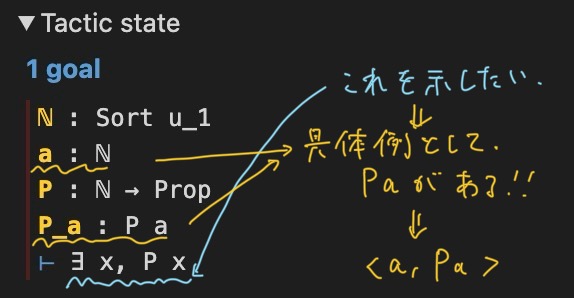
この式だけではイメージが湧きづらいかもしれないので, intro_existsのexactを使う前の状態を出してみました. 今, ∃x, P xの具体例としてP aを持っているため, Anonymous constructorを使って型∃x, P xをもつものを生成できます.
このAnonymous constructorですが, 実はこれを使って∃から具体例を引き出したり, ∧を分解したりできます. 例えば, ∧ならば以下のように分解することができます. この例ではa_and_b: A ∧ Bをa: Aとb: Bに分解しています.
theorem destruct_and: A ∧ B → A := by
intros a_and_b
let ⟨a, b⟩ := a_and_b
exact a
∃も同様に分解でき, ある値とその値が持つ性質に分解することができます. 例えばP_x: ∃x, P xである時に,
let ⟨a, P_a⟩ := P_x
とすれば, aとP_a: P aを得ることができます.
また, パターンマッチングのようにAnonymous constructorはネストすることができます. つまり, P_and_Q_x: ∃x, P x ∧ Q xのようなものが与えられた時も
let ⟨a, ⟨P_a, Q_a⟩⟩ := P_and_Q_x
のように一度に分解できます.
分解のためにわざわざそれ専用の定理を持ってこないで済みますし, 何より関数型言語のパターンマッチングのように直感的なので個人的にこの記法を重宝しています.
5. by_contra 見出しへのリンク
by_contraはby_contradictionのエイリアスで背理法を用いたい時に使えるtacticです. 例えば, x ∈ Pが証明のゴールの時に,
by_contra not_x_in_P
と記述すると, not_x_in_P: x ∉ Pが仮定に追加され, ゴールがFalseに変化します. これはまさに背理法でやっていることそのものになります.
あとはnot_x_in_Pを使って適当にFalseを導きましょう. 否定が出てきた時は¬AがA → Falseと同値であることを使って, Modus PonensからFalseを導きましょう.
6. by_cases 見出しへのリンク
by_casesは場合分けに使えるtacticです. 例えば, x ∈ Pかどうかで場合分けをしたい場合は,
by_cases x_in_P: x ∈ P
case pos =>
/- x ∈ Pである時の証明 -/
case neg =>
/- x ∉ Pである時の証明 -/
のように書くことができます. 注意として, posの場合はx_in_P: x ∈ Pが仮定として追加されますが, negの場合はx_in_P: x ∉ Pが仮定として追加されます. 自分はposの時に合わせて命名を行っていますが, そうすると否定の場合の証明で混乱を招く可能性があるので注意しましょう.
by_casesではいずれの場合も同じゴールを目指すことになりますが, このように証明が「分岐する」場合はそれぞれ異なるゴールを証明する必要がある場合があるので, 今自分が示すべきゴールを意識する必要があります.
7. choose 見出しへのリンク
https://leanprover-community.github.io/mathlib4_docs/Init/Classical.html#Classical.choose
chooseはいわゆる選択関数です. ∃a, P aの形の式から実際のaを取り出すことのできる関数です. 例えば, Pを引数としてP aを満たすaを返すような関数を構成したい時に使えます. ここでわざわざ取り上げたのは, 自分がchooseの存在を知らず, 先ほどのanonymous constructorをうまく使えば書けるだろうと考えてかなりの時間を溶かしたためです.
証明に用いる際は, chooseで得られた値がちゃんと条件を満たすことを言ってくれるchoose_specという定理と合わせて使いましょう. また, 選択関数を取るには古典論理が必要なので注意しましょう.
余談ですが, chooseとは先ほど紹介したMathlib4のドキュメントを漁って出会いました.
8. rewrite (config := {occs := .pos [n]}) 見出しへのリンク
この記事で私が最も伝えたい内容です.
まず, 前提として, Lean4のrewriteはある変数の出現を全て書き換えます. 例えば, 現在の状況が以下のようになっている時にrewrite [←a_eq_b]すると
a_eq_b : a = b
⊢ f b + g b = a + a
が
a_eq_b : a = b
⊢ f a + g a = a + a
となります. この性質は基本的には式からある変数をまとめて除去できるので嬉しいですが, たまに特定の変数のみを書き換えたい場合が存在します. 上の例であれば2番目のbのみを書き換えてf b + g a = a + aを得たい場合が存在します.
このような時に使えるのが, rewrite (config := {occs := .pos [n]})です. このrewriteのオプションを使うと, 変数の特定の出現のみを書き換えるよう指示することができます. 例えば先ほどの例であれば,
rewrite (config := {occs := .pos [2]}) [←a_eq_b]
とすると, bの2番目の出現のみを書き換えてf b + g a = a + aを得ることができます.
このようなrewriteの使い方は, 私が探した範囲ではドキュメントにもなく日本語の資料も見当たらず, 散々探した末にたどり着いた Rewriting certain terms in Lean4 - Proof Assistants Stack Exchange から知ることができました. あまり使う場面に遭遇することはありませんが, 知らないとどうしようもない場合があるので知っておいて損はないと思います.
もしかしたら私の目が節穴なだけかもしれないので, rewriteのconfigに関するドキュメントを見つけた方がいらっしゃれば教えてもらいたいです.
まとめ 見出しへのリンク
自分のメモに記してあった備忘録をそのまま書き起こしたので, 予想以上に統一感のない内容になってしまいました. それでも, ここに出てきた内容のうちどれか1つでも役に立てば幸いです.
(余談) ISer向け 見出しへのリンク
せっかくなので3Sの「情報論理演習」の証明課題もLean4で証明してそのまま提出したら単位を貰えました. 適当なことは言えないので, もしこの記事を見てLean4に興味をもった方がいるなら, 一度指導教官にLean4での提出が認められるかは確認した方が良いと思います. Lean4で証明を書くと手で証明を書くより数割増で楽しい(個人差あり)のでおすすめです.
Lean4の処理系が健全かどうかの証明を要求されることはありませんでしたのでそこは安心してください.
参考 見出しへのリンク
leanprover-community/mathlib4 - Github Mathlib4 Docs Rewriting certain terms in Lean4 - Proof Assistants Stack Exchange